Площадь кольца формула: Площадь кольца онлайн расчет и формула

Содержание

Площадь кольца — формула, пример расчета

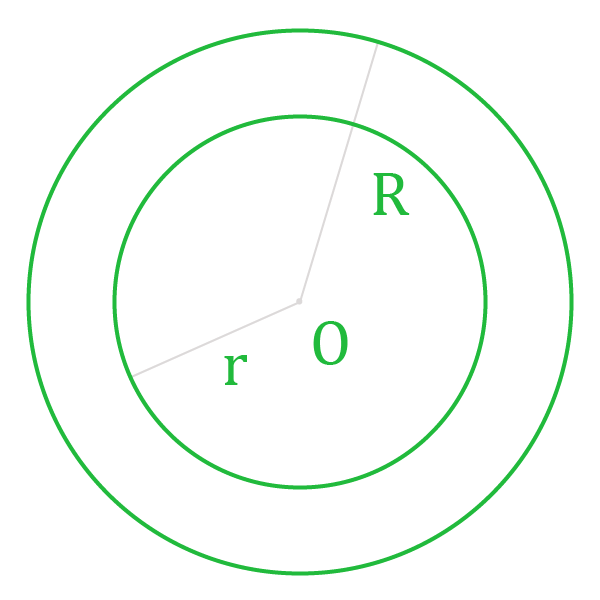
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус.

Площадь кольца, выраженная через внешний и внутренний радиусы

Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Фигура, заключенная между этими окружностями и будет кольцо, у которого R является внешним радиусом, r -внутренним радиусом.
Тогда площадь этой фигуры будет равна разницы между площадью круга с большим радиусом и площадью круга с меньшим радиусом.

Площадь круга с радиусом r выражается формулой:

Площадь круга с радиусом R выражается формулой:

Тогда площадь кольца будет равна:

Таким образом, площадь кольца равна произведению числа на разницу квадратов внешнего и внутреннего радиусов:

Пример расчета площади кольца, если известны его радиусы.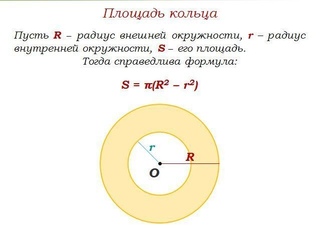

Найдите площадь кольца, если его внешний радиус равен 3, а внутренний – 2
Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площадь кольца, выраженная через внешний и внутренний диаметры

Иногда при решении задач удобней использовать формулу площади кольца, выраженную через внутренний и внешний диаметры.

Пусть D – внешний диаметр кольца, d -внутренний диаметр кольца, тогда:

Выразим радиус через диаметр. Имеем:

Площадь кольца вычисляется по формуле:

Подставив выраженные через диаметр радиусы, получим:

Таким образом, площадь кольца равна четверти произведения числа на разницу квадратов внешнего и внутреннего диаметров:

Пример расчета площади кольца, если известны его диаметры.

Найдите площадь кольца, если его внешний диаметр равен 10, а внутренний – 6
Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площади кольца, выраженная через средний радиус и ширину кольца

Пусть k– ширина кольца, являющийся разницей между большим и меньшим радиусом, то есть k=R-r-средний радиус кольца, равный

Площадь кольца вычисляется по формуле:

Применив формулу разности квадратов, имеем:

Но R-r=k, а
Подставим правые части равенства в формулу площади кольца.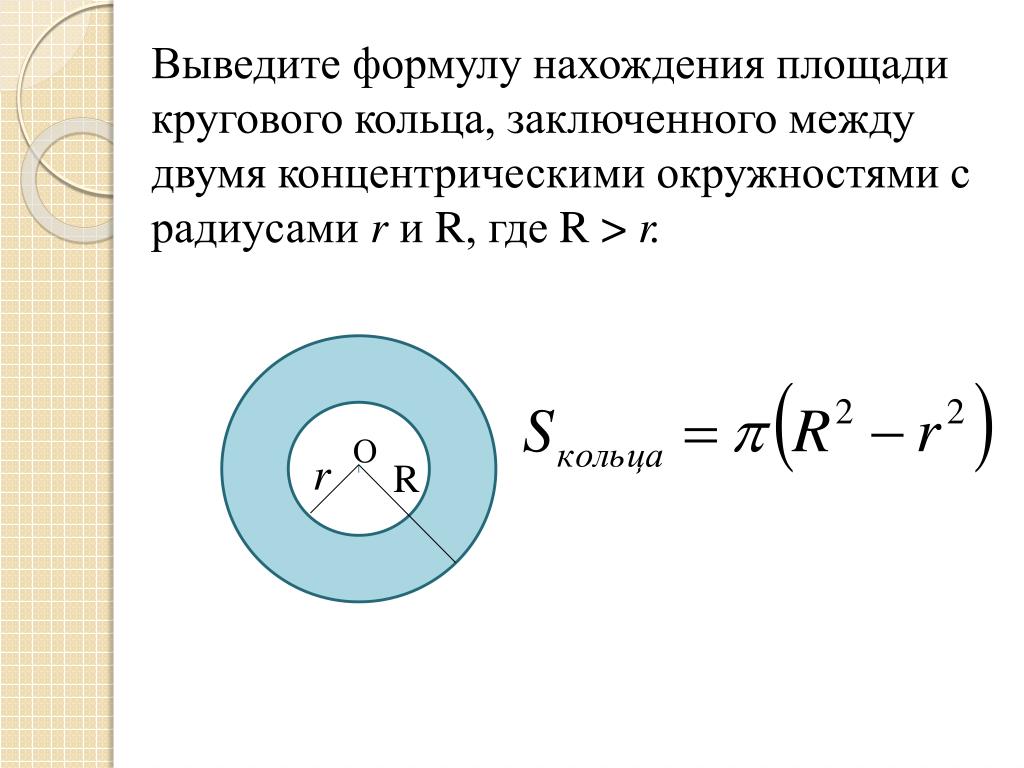
Получим:

Площадь кольца равна удвоенному произведению числа среднего радиуса на ширину кольца.

Пример расчета площади кольца, если известны его средний радиус и ширина.
Найдите площадь кольца, если его средний радиус равен 5, а ширина – 2

Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площади кольца через длину самого большого отрезка, проведенного внутри кольца

Пусть AB –самый большой отрезок, лежащий внутри кольца. Точка С – половина этого отрезка. Этот отрезок будет являться касательной к кругу меньшего радиуса. Касательная перпендикулярна радиусу меньшей окружности, проведенного в точку каcания C. Тогда
Следовательно, треугольник ACO –прямоугольный, где

По теореме Пифагора имеем:

Площадь кольца равна:

Подставив, получим:

Следовательно, площадь кольца равна произведению числа на квадрат половины самого большого отрезка кольца.

Площадь кольца — онлайн калькулятор

Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Площадь кольца по радиусам или диаметрам

Просто введите радиусы или диаметры окружностей, и получите ответ.

Площадь кольца по толщине и любому другому параметру

Просто введите толщину кольца и любой другой известный вам параметр, и получите ответ.

Теория

Площадь кольца через радиусы

Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности

R и радиус внутренней окружности r ?

Формула

S = π ⋅ (R² — r²)

Пример

К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:

S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²

Ответ: S = 15.7 см²

Площадь кольца через диаметры

Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?

Формула

S = ^π/₄ ⋅ (D² — d²)

Пример

К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:

S = 3. 14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²

Ответ: S = 9.42 см²

Площадь кольца через толщину

Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:

внешний диаметр D
внутренний диаметр d
радиус внешней окружности R
радиус внутренней окружности r

Формулы

S = ^π/₄ ⋅ (D² — (D — 2t)²)

S = ^π/₄ ⋅ ((d + 2t)² — d²)

S = π ⋅ (R² — (R — t)²)

S = π ⋅ ((r + t)² — r²)

Пример

Для примера, найдём чему равна площадь кольца толщиной

t = 2 см и внешним диаметром D = 5 см:

S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²

См. также

Формула площади кольца

Кольцо, это геометрическая фигура, которая имеет внешний радиус R и внутренний радиус r с общим центром. В повседневной жизни с кольцами приходится встречаться не так уж и редко, поскольку они являются необходимыми элементами многих технических устройств, которыми пользуются практически все. Еще чаще с кольцами имеют дело инженеры и конструкторы, создающие всевозможные машины, узлы и агрегаты.

Расчет площади кольца

Формула расчёта площади кольца

Найти площадь кольца можно по формуле:

S = π ( R²− r²)

R – радиус внешней окружности

r – радиус внутренней окружности

S – площадь кольца

π – 3.14

Форму колец имеют шайбы, являющимися элементами крепежа, которые устанавливаются между головками болтов или гаек и скрепляемых изделий для того, чтобы увеличить площадь прилегания, а также для того, чтобы предотвратить самопроизвольное отвинчивание.

Если требуется в том или ином случае рассчитать или подобрать для установки в изделие именно ту шайбу, которая необходима, конструкторам нужно, помимо всего прочего, найти площадь кольца. Эти детали чаще всего изготавливаются из стали, цветных металлов или пластмасс и могут иметь как плоскую, так и специальную поверхность. Во втором случае шайбы производятся из пружиненной стали, называемые гроверными шайбами которые служат для предотвращения ослабления резьбовых соединений при тряске и вибрациях.

Большое распространение в технике получили также и

уплотнительные кольца. Они предназначаются для того, чтобы обеспечить герметизацию соединений в трубопроводах, по которым производится транспортировка газов или жидкостей, а также в пневматических и гидравлических агрегатах. Устанавливаются они в местах соединений различных деталей и благодаря своей эластичности очень плотно прилегают к поверхностям, между которыми располагаются. Наиболее распространенным материалом для изготовления уплотнительных колец является резина различных сортов и составов, а также некоторые специальные виды пластических масс.

Практически все современные двигатели внутреннего сгорания имеют в своей конструкции такие важные элементы, как

поршневые кольца. Эти детали нужны для того, чтобы достичь необходимой степени компрессии в камере сгорания и располагаются между поршнями и стенками цилиндров. Поскольку при работе силовых агрегатов они испытывают постоянное трение, то со временем изнашиваются и требуют замены. Изготавливаются поршневые кольца чаще всего из высококачественного серого чугуна.

Еще одной разновидностью колец являются стопорные кольца. Они используются для фиксации различных механических деталей и почти всегда устанавливаются в специально проточенных для них канавках. Чаще всего стопорные кольца можно встретить на валах, однако нередко они располагаются и в корпусах деталей. В зависимости от местонахождения они подразделяются на те, которые предназначены для вала и те, которые монтируются в отверстиях, а что касается материала изготовления этих деталей, то им чаще всего является сталь.

После установки на свое «законное» место стопорное кольцо обычно немного разжимается и своими торцевыми поверхностями препятствует смещению деталей друг относительно друга.

Задача B5: площадь кольца

3 октября 2013

Сегодня мы разберем нестандартную

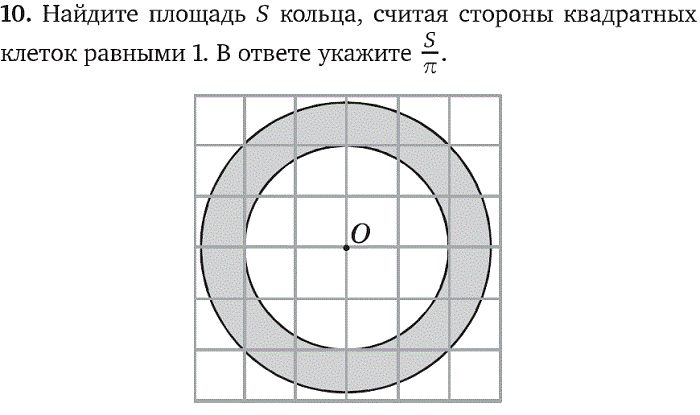
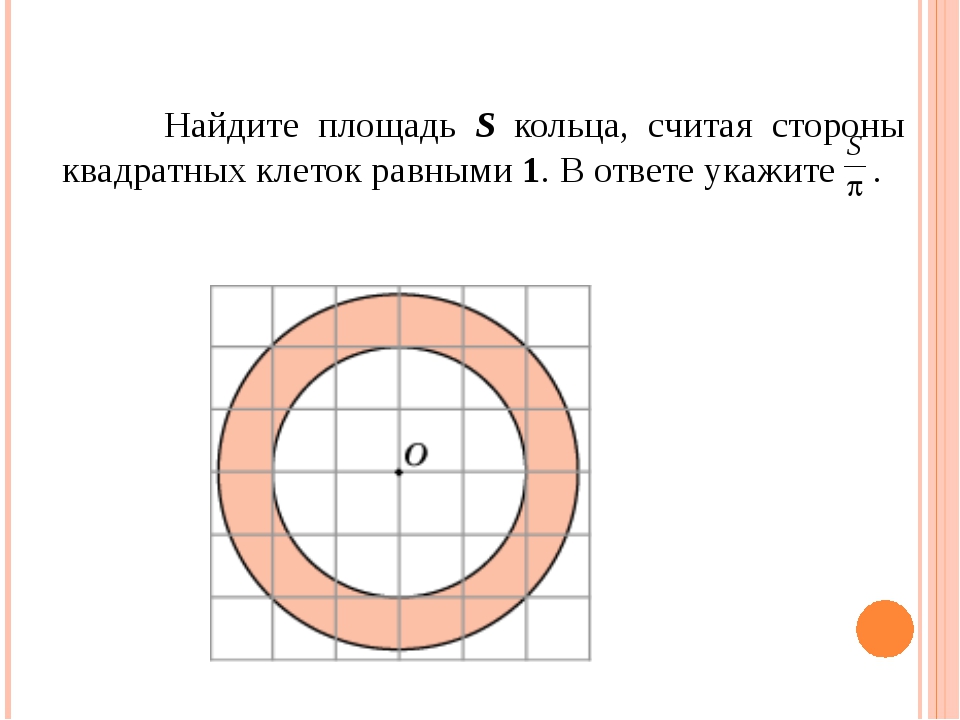
задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:

Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:

S = πR²

где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R₁, а внешний радиус — R₂. Внутренний радиус очень легко считается, он равен двум клеточкам:

R₁ = 2 ⇒ R₁² = 4

Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:

Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:

По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:

R² = OA² = OC² + AC² = 2² + 2² = 4 + 4 = 8

Итого мы получили:

R₂² = 8

Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:

S₁ = πR₁² = π · 4 = 4π;
S₂ = πR₂² = π · 8 = 8π.

Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S₂ вычесть площадь меньшего круга S₁. Получаем:

S = S₂ − S₁ = 8π − 4π = 4π

Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:

S/π = 4π/π = 4

Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.

Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)

Смотрите также:

Нестандартная задача B5 на площадь круга
Задача B5: площадь закрашенного сектора
В 2012 году ЕГЭ по математике станет двухуровневым?
Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
Подготовка к ЕГЭ по математике
Задача B2 про комиссию в терминале

Площади кругов и окружностей

Формула площади круга, диаметр

r — радиус круга

D — диаметр

π ≈ 3. 14

Площадь сегмента круга

Формула площади сегмента круга (S), отсекаемая хордой AC:

R — радиус круга

α — угол сегмента в градусах

π = 3.14

Площадь кольца

Формула площади кольца (S):

R — радиус внешней окружности

r — радиус внутренней окружности

π = 3.14

Площадь сектора кольца

Формула площади сектора кольца (S):

R — радиус внешней окружности

r — радиус внутренней окружности

α — угол сектора AOB, в градусах

π = 3.14

Записи по теме

Площади поверхностей Формулы площади поверхностей объёмных фигур.

Формулы для расчёта площади поверхности куба, прямоугольного параллелепипеда, правильной и усечённой пирамид, усечённого конуса. Площади фигур Формулы для расчёта площадей двумерных геометрических фигур. Площадь треугольника, квадрата, параллелограмма, ромба, трапеции, правильного многоугольника.

Формула площади круга через диаметр или радиус или длину окружности

Длина через радиус

Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга.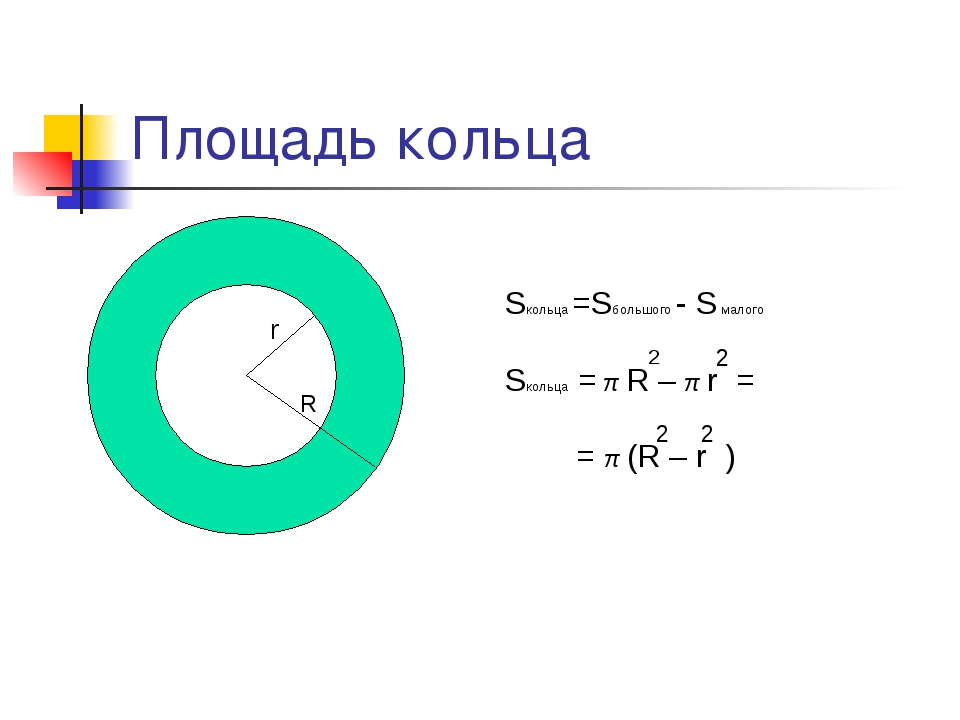 Предположим, что C – это длина окружности, r – ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.

Задача про увеличение длины экватора

Следующую задачу интересно будет задать своим друзьям или кому-то из взрослых. Очень часто на нее дают неправильный ответ. Но мы-то, конечно, в ней ошибаться не будем.

Представим, что экватор Земли – это металлический обруч. Мы его распили и вставили туда один дополнительный метр. И равномерно распределили по всей длине. Получился зазор. (См. Рис. 11.)

Рис. 11. Зазор между окружностями

Вопрос: насколько большой этот зазор? Может ли туда, например, пролезть кошка?

Если не задумываться над пропорциональностью длины окружности и радиуса, то кажется, что этот зазор будет очень мал, его даже не будет видно. Ведь мы этот дополнительный метр распределили по всей длине экватора, а это км.

Но посчитаем.

Итак, экватор Земли равен , а радиус – .

Увеличим экватор на м, обозначим его , и найдем радиус новой окружности :

Радиус новой окружности больше старого примерно на см. Но это ведь и есть тот самый зазор между двумя окружностями. Конечно, кошка в такой зазор пролезть сможет.

В реальности эту задачу можно применить вот в какой ситуации. Есть достаточно длинная кольцевая дорога, например вокруг стадиона. Вы идете по внешнему тротуару. (См. Рис.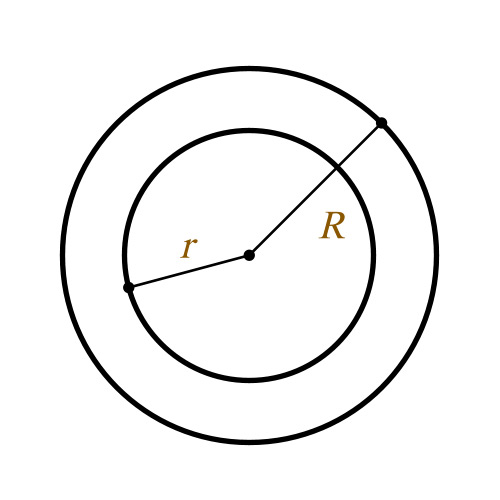 12.) Вопрос: если перейдете дорогу и пойдете по внутреннему тротуару, то насколько это сократит вам дорогу?

Рис. 12. Дорога вокруг стадиона

Если ширина дороги метров, то, переходя дорогу, вы уменьшаете радиус на метров, значит, длина всей дороги уменьшается на .

Как найти длину окружности через радиус

Умножьте число пи на два радиуса.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
r — радиус окружности.

3. Как вычислить длину окружности через площадь круга

Умножьте число пи на четыре площади круга.

Найдите корень из результата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

4. Как найти длину окружности через диагональ вписанного прямоугольника

Умножьте число пи на диагональ.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d – любая диагональ прямоугольника.

5. Как вычислить длину окружности через сторону описанного квадрата

Умножьте число пи на сторону квадрата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
a – любая сторона квадрата.

6. Как найти длину окружности через стороны и площадь вписанного треугольника

Перемножьте стороны треугольника.

Поделите результат на площадь и на два.

Умножьте полученное число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
a, b, c – стороны треугольника.

7. Как найти длину окружности через площадь и полупериметр описанного треугольника

Поделите площадь треугольника на его полупериметр.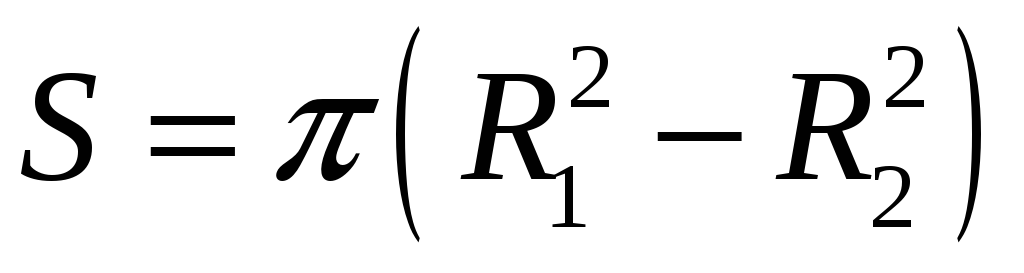

Умножьте результат на число пи и на два.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
p – полупериметр треугольника (равен половине от суммы всех сторон).

8. Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.

Найдите синус полученного числа.

Разделите сторону многоугольника на результат.

Умножьте получившееся число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
π (пи) — константа, равная 3,14.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Число π

Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:

	Ведро	Таз	Бочка	Тарелка	Стакан
Окружность	91 см	157 см	220 см	78,5 см	23,9 см
Диаметр	29 см	50 см	70 см	25 см	7,6 см
Отношение (с точн. до 0,01)	3,14	3,14	3,14	3,14	3,14

Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π.

Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π. В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.

Длина окружности и площадь круга

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):

Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

C = πD = 2πR

где C – длина окружности, π – константа, D – диаметр окружности, R – радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

C ≈ 3,14 · 5 = 15,7 (см)

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Сначала найдём диаметр окружности, умножив длину радиуса на 2:

D = 3,5 · 2 = 7 (м)

теперь найдём длину окружности, умножив π на диаметр:

C ≈ 3,14 · 7 = 21,98 (м)

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π

следовательно радиус будет равен:

R	≈	7,85	=	7,85	= 1,25 (м)
2 · 3,14	6,28

Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:

S = πr2

где S – площадь круга, а r – радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

S = π(	D	)2 = π	D2	= π	D2
2	22	4

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2)

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Сначала найдём радиус круга, разделив его диаметр на 2:

7 : 2 = 3,5 (см)

теперь вычислим площадь круга по формуле:

S = πr2 ≈ 3,14 · 3,52 = 3,14 · 12,25 = 38,465 (см2)

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D2	≈ 3,14	72	= 3,14	49	=	153,86	= 38,465 (см2)
4	4	4	4

Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.

Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:

r = √S : π

следовательно радиус будет равен:

r ≈ √12,56 : 3,14 = √4 = 2 (м)

Число π

Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно.

Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.

В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

Ведро	Таз	Бочка	Тарелка	Стакан
Окружность	91 см	157 см	220 см	78,5 см	23,9 см
Диаметр	29 см	50 см	70 см	25 см	7,6 см
Отношение (с точн.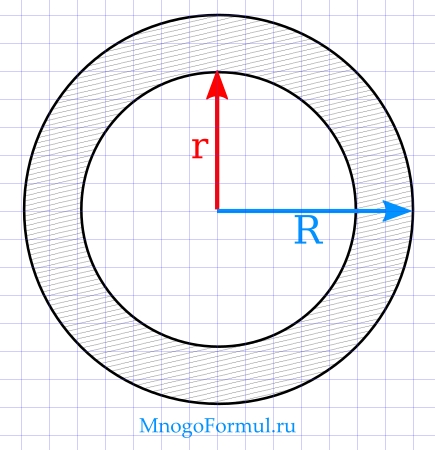 до 0,01)	3,14	3,14	3,14	3,14	3,14

Шаг 5

Аналогично найдем площадь многоугольника Р₂.

Соединим центр с вершинами описанного многоугольника.

Так как многоугольник правильный, то получим n равных треугольников. Площадь многоугольника будет равна сумме площадей образованных треугольников. Так как всего n равных треугольников, то площадь Р₂ будет в n раз больше:

Рассмотрим равнобедренный треугольник КОТ.

Он является равнобедренным, так как точка О – центр вписанной в него окружности, следовательно, О равноудалена от вершин многоугольника.

Площадь треугольника КОТ можно найти с помощью формулы через основание и высоту:

OA является высотой, так как А – точка касания окружности и прямой КТ, а радиус окружности перпендикулярен прямой в точке касания.

Так как треугольник КОТ – равнобедренный, то высота ОА будет и медианой, следовательно:

По построению, ОА – радиус вписанного многоугольника Р₁.

Тогда формулу площади треугольника КОТ можем переписать:

Площадь кольца, выраженная через внешний и внутренний диаметры

Иногда при решении задач удобней использовать формулу площади кольца, выраженную через внутренний и внешний диаметры.
Пусть D – внешний диаметр кольца, d -внутренний диаметр кольца, тогда:
Выразим радиус через диаметр. Имеем:
Площадь кольца вычисляется по формуле:
Подставив выраженные через диаметр радиусы, получим:
Таким образом, площадь кольца равна четверти произведения числа на разницу квадратов внешнего и внутреннего диаметров:

Пример расчета площади кольца, если известны его диаметры.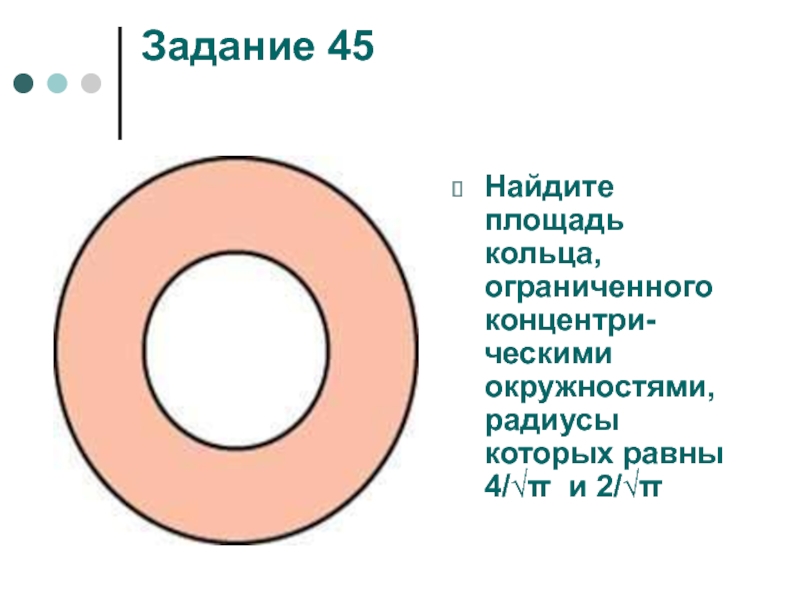
Найдите площадь кольца, если его внешний диаметр равен 10, а внутренний – 6
Площадь кольца вычисляется по формуле:
Подставив значения из условия задачи, имеем:

Шаг 10

Итак, многоугольник Р₁ содержащийся в круге, имеет площадь (шаг 4):

а многоугольник Р₂ содержащий круг, имеет площадь (шаг 9):

Где:

P_P₁ – периметр многоугольника Р_1,

R – радиус круга,

α – половина центрального угла многоугольника Р₁.

При достаточно большом n периметр многоугольника (P_P₁) отличается сколь угодно мало от длины окружности (l).

cos α сколь угодно мало отличается от единицы. Так как при увеличении n центральный угол многоугольника уменьшается, а его половинный угол становится еще меньше (α-половина центрального угла по построению). Значит угол α стремится к нулю. Косинус нуля равен 1. Поэтому, мы и говорим, что при увеличении n косинус α сколь угодно мало отличается от единицы.

Тогда получаем, что площади многоугольников Р₁и Р₂ сколь угодно мало отличаются от:

При помощи пределов это можно записать следующим образом:

и:

В свою очередь площадь круга при достаточно большом n сколь мало отличается от площадей этих многоугольников. Значит, можем записать формулу площади круга:

Воспользуемся формулой длины окружности через радиус и π:

Формула площади круга примет вид:

Формулы площади круга выведены.

Найдите площадь круга

В прошлой статье мы с вами разобрали, как быстро восстановить в памяти формулы площади сектора круга, длины дуги окружности, площади сегмента круга. Первые две формулы как раз нам понадобятся для решения ряда заданий связанных с кругом.

Рассмотренные ниже задачи на первый взгляд могут показаться не очень простыми, но зная оговоренные выше формулы и используя простую логику решение осуществите без труда. Примеры не представляют никакой сложности. Необходимо помнить сами формулы (или быстро восстановить их в памяти), и путём простейших преобразований выразить радиус или центральный угол. Рассмотрим задачи:

Найдите площадь круга, длина окружности которого равна .

Формула площади круга:

Формула длины окружности:

Для того, чтобы найти площадь круга, необходимо найти радиус круга, его мы можем найти используя формулу длины окружности, подставляем данное в условии значение:

Подставим найденный радиус в формулу площади круга и найдём её:

Ответ: 625

Площадь круга равна . Найдите длину его окружности.

Формула площади круга:

Формула длины окружности:

Это задача обратная предыдущей. Для нахождения длины окружности необходимо используя формулу площади круга найти его радиус. Сделаем это:

Значит длина окружности равна:

Ответ: 1

Найдите площадь сектора круга радиуса , центральный угол которого равен 90⁰.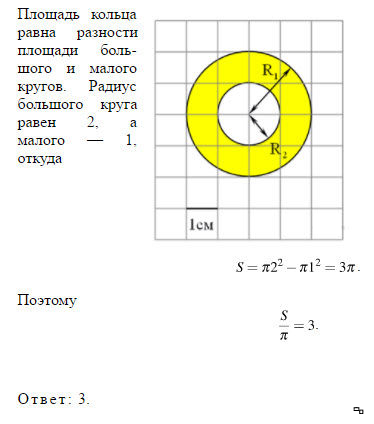

Формула площади круга:

Сектор круга с центральным углом 90 градусов составляет четвёртую часть от целого круга. Вообще, площадь сектора круга определяется по формуле:

Ответ: 20,25

Найдите площадь сектора круга радиуса 41, длина дуги которого равна 2.

Площадь сектора круга определяется по формуле:

Длина дуги сектора:

Для нахождения площади сектора нам необходимо найти центральный угол n. Его мы можем найти используя формулу длины дуги:

Подставляем:

Ответ: 41

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и .

Формула площади круга:

Нам необходимо вычислить площадь большего круга и площадь меньшего круга, найти разность. Эта разность будет являться площадью кольца:

Ответ: 336

Найдите центральный угол сектора круга радиуса , площадь которого равна 375. Ответ дайте в градусах.

Площадь сектора круга определяется по формуле:

Подставим известные величины:

Ответ: 150

Посмотреть решение

На этом всё. В данной рубрике мы продолжим рассматривать задачи, не пропустите!Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Площадь круглого кольца или кольцевого пространства

Кольцевое пространство :

Круговое кольцо (кольцо) — это плоская фигура, ограниченная по окружности двумя концентрическими окружностями двух разных радиусов. Площадь круглого кольца определяется путем вычитания площади малого круга из площади большого круга. 2}) = \ pi (R — r) (R + r) \]

i.е. , чтобы найти площадь кольца (или кольца), умножьте произведение суммы и разности двух радиусов на $$ \ pi $$ в первом рисунке.

Примечание: Правило остается в силе, даже если окружности не концентрические, как на втором рисунке.

Пример :

Дорожка шириной $ 14 $$ см окружает круглый газон диаметром $ 360 $ см. Найдите участок пути.

Решение :

Учитывая, что
Радиус внутреннего круга $$ = 180 $$ см
Радиус внешнего круга $$ = (180 + 14) = 194 $$ см
$$ \ поэтому $$ площадь пути $$ = \ pi ( R — r) (R + r) $$
$$ = \ frac {{22}} {7} (194 + 180) (194 — 180) = 16456 $$ Квадрат в см

Пример :

Площадь двух концентрических окружностей составляет 1386 долларов на квадратный сантиметр и 1886 долларов. 2} = 1386 $$ кв. См
$$ \ поэтому $$ $$ \ log \ pi + 2 \ log r = \ log 1386 $$
$$ 2 \ log r = \ log 1386 — \ log (3.143) $$
$$ = 3,1418 — 0,4973 = 2,6454 $$
$$ \ log r = 1,3223 $$
$$ r = анти \ log (1,3223) = 21 $$

Отсюда ширина кольца $$ = R — r = 24,51 — 21 = 3,51 $$ см

Площадь круга — формула, примеры, определение

Площадь круга — это пространство, занимаемое кругом в двухмерной плоскости. В качестве альтернативы пространство, занимаемое в пределах границы / окружности круга, называется площадью круга.Формула для вычисления площади круга: A = πr ², где r — радиус круга. Единицей площади является квадратная единица, например, м ², см ², в ² и т. Д. Площадь круга = πr ² или πd ²/4 в квадратных единицах, где (Pi) π = 22/7 или 3,14. Пи (π) — это отношение длины окружности к диаметру любой окружности. Это особая математическая константа.

Формула площади круга полезна для измерения области, занятой круговым полем или графиком.Предположим, у вас есть круглый стол, тогда формула площади поможет нам узнать, сколько ткани нужно, чтобы покрыть его полностью. Формула площади также поможет нам узнать длину границы, то есть длину окружности. Есть ли у круга объем? Нет, у круга нет объема. Круг — это двухмерная форма, у него нет объема. У круга есть только площадь и периметр / окружность. Давайте подробно узнаем о площади круга, площади поверхности и его окружности на примерах.

Круг и части круга

Круг — это набор точек, находящихся на фиксированном расстоянии от центра круга. Круг — это замкнутая геометрическая фигура. В повседневной жизни мы видим круги, такие как колесо, пицца, круглая площадка и т. Д. Мера пространства или области, заключенная внутри круга, известна как площадь круга.

Радиус : Расстояние от центра до точки на границе называется радиусом окружности.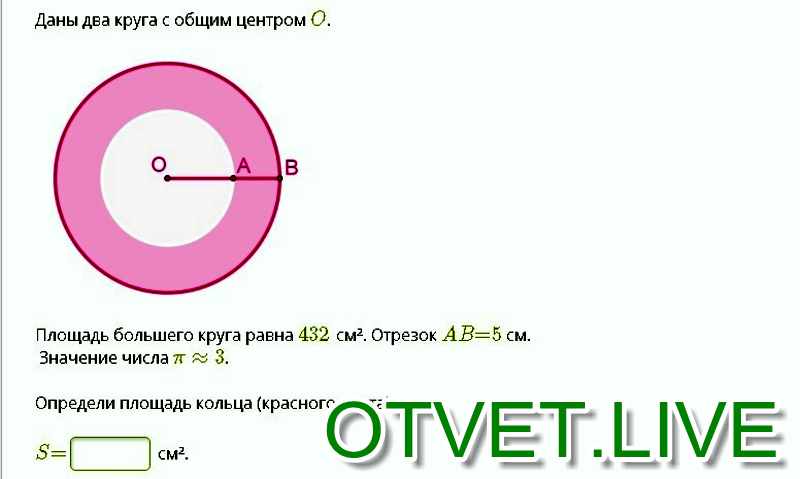 Он обозначается буквой «r» или «R». Радиус играет важную роль в формуле площади и окружности круга, которую мы узнаем позже.

Диаметр : Линия, проходящая через центр, а ее конечные точки лежат на окружности, называется диаметром окружности. Он обозначается буквой «d» или «D».

Диаметр: Диаметр круга в два раза больше его радиуса. Диаметр = 2 × Радиус

d = 2r или D = 2R

Если диаметр круга известен, его радиус можно рассчитать как:

r = d / 2 или R = D / 2

Окружность: Окружность круга равна длине его границы.Это означает, что периметр круга равен его длине окружности. Длина веревки, которая идеально обвивает границу круга, будет равна его длине. Приведенный ниже рисунок поможет вам представить то же самое. Окружность можно измерить по следующей формуле:

, где r — радиус круга, а π — математическая константа, значение которой приблизительно равно 3,14 или 22/7. Окружность круга может использоваться, чтобы найти площадь этого круга.

Для окружности радиуса «r» и окружности «C»:

π = Окружность / Диаметр
π = C / 2r = C / d
С = 2πr

Давайте разберемся в различных частях круга на следующем примере из реальной жизни.

Рассмотрим парк круглой формы, как показано на рисунке ниже. Мы можем идентифицировать различные части круга с помощью рисунка и таблицы, приведенных ниже.

По кругу	В нашем парке	Обозначается буквой
Центр	Фонтан	Ф
Окружность	Граница
Хорда	Вход в игровую зону	PQ
Радиус	Расстояние от фонтана до Въездных ворот	FA
Диаметр	Прямая линия Расстояние между входными и выходными воротами через фонтан	AFB
Малый сегмент	Меньшая часть парка, обозначенная как Игровая зона
Основной сегмент	Большая территория парка, кроме игровой
Внутренняя часть круга	Зеленая зона всего парка
Наружная часть круга	Территория за границей парка
Дуга	Любая изогнутая деталь по окружности.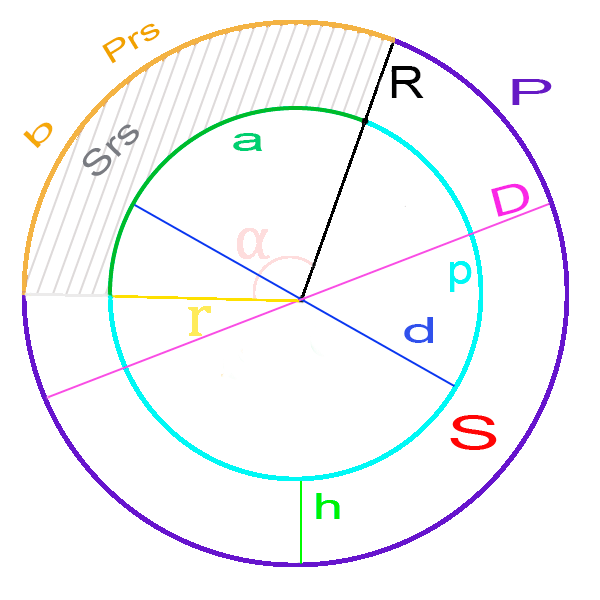

Что такое площадь круга?

Площадь круга — это пространство, заключенное в пределах круга. Область внутри круга — это область, занятая кругом. Его также можно назвать общим количеством квадратных единиц внутри этого круга.

Формулы площади круга

Площадь круга может быть вычислена промежуточными шагами по диаметру и длине окружности.По диаметру и длине окружности мы можем найти радиус, а затем площадь круга. Но эти приведенные выше формулы предоставляют самый короткий способ найти площадь круга. Предположим, что круг имеет радиус ‘r’, тогда площадь круга = πr ² или πd ²/4 в квадратных единицах, где π = 22/7 или 3,14, а d — диаметр.

Площадь круга, A = πr ² квадратных единиц

Окружность / Периметр = 2πr единиц

Площадь круга можно рассчитать по формулам:

Площадь = π x r ², где r — радиус.
Площадь = (π / 4) x d ², где d — диаметр.
Площадь = C ² / 4π, где C — длина окружности.

Площадь круга с использованием диаметра

Площадь круга по диаметру равна: Площадь круга = πd ²/4. Здесь d — диаметр круга. Диаметр круга в два раза больше радиуса круга. г = 2р. Обычно, исходя из диаметра, нам нужно сначала найти радиус круга, а затем найти площадь круга.С помощью этой формулы мы можем напрямую найти площадь круга из меры диаметра круга.

Площадь круга по окружности

Площадь круга относительно окружности определяется формулой. (Окружность круга) ²/4 \ (\ pi \). Есть два простых шага, чтобы найти площадь круга по заданной длине окружности. Окружность круга сначала используется, чтобы найти радиус круга. Этот радиус также помогает найти площадь круга.Но в этих формулах мы сможем напрямую найти площадь круга по его длине.

Площадь круга — расчет

Площадь круга можно удобно рассчитать по радиусу, диаметру или длине окружности. Константа, используемая при вычислении площади круга, равна пи, и имеет дробное числовое значение 22/7 или десятичное значение 3,14. Любое из значений пи может использоваться в зависимости от требований и потребностей уравнений.В таблице ниже показан список формул, если мы знаем радиус, диаметр или длину окружности.

Площадь круга с известным радиусом.	πr ²
Площадь круга с известным диаметром.	πd ²/4
Площадь круга с известной длиной окружности.	С ²/ 4π

Определение площади круга

Почему площадь круга равна πr ²? Чтобы понять это, давайте сначала разберемся, как выводится формула для площади круга.

Круг можно разрезать на треугольник, радиус которого равен высоте треугольника, а периметр — его основанию, равному 2πr. Мы знаем, что площадь треугольника определяется путем умножения его основания на высоту, а затем деления на 2, что составляет 1/2 x 2πr xr = πr ^2. Следовательно, площадь круга равна πr ² , где r — радиус окружности, а значение π равно 22/7 или 3,14.

Формула площади поверхности круга

Площадь поверхности круга такая же, как площадь круга.Фактически, когда мы говорим площадь круга, мы имеем в виду не что иное, как общую площадь его поверхности. Площадь поверхности — это площадь, занимаемая поверхностью трехмерной формы. Поверхность сферы будет иметь сферическую форму, но круг — это простая плоская 2-мерная форма.

Если дана длина радиуса или диаметра, или даже длина окружности круга, то мы можем узнать площадь поверхности. Он представлен в квадратных единицах. Площадь поверхности круга = πr ², где r — радиус круга, а значение π приблизительно равно 3.14 или 22/7.

Пример из реального мира

Рон и его друзья заказали пиццу в пятницу вечером. Каждый срез имел длину 15 см.

Вычислите площадь пиццы, которую заказал Рон. Вы можете предположить, что длина кусочка пиццы равна радиусу пиццы.

Решение:

Пицца имеет круглую форму. Таким образом, мы можем использовать формулу круга для вычисления площади пиццы.

Радиус 15 см

Площадь круга = πr ² = 3.14 х 15 х 15 = 706,5

Площадь пиццы = 706,5 кв. См.

Часто задаваемые вопросы о площади круга

Как рассчитать площадь круга?

Площадь круга можно рассчитать по формулам:
Площадь = π x r ², где r — радиус.
Площадь = (π / 4) x d ², где d — радиус.
Площадь = C ² / 4π, где C — длина окружности.

Что такое формула площади круга?

Площадь = π x r ².Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга при заданном радиусе r равна πr ². Площадь круга при известном диаметре d равна πd ²/4.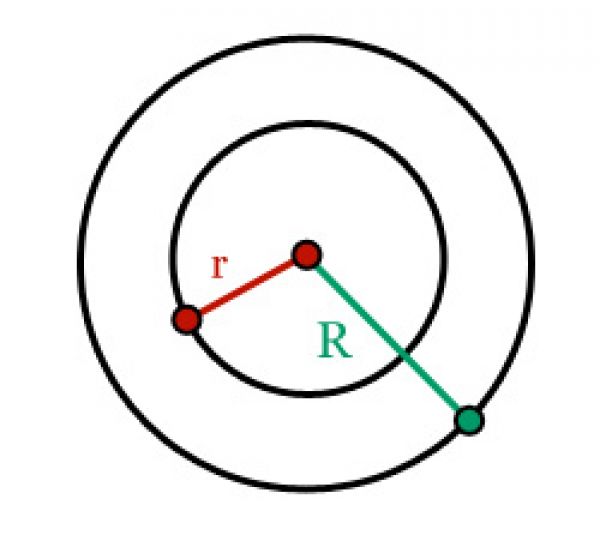 π составляет примерно 3,14 или 22/7.

Площадь (A) также может быть найдена по формулам A = (π / 4) x d ², где d — радиус, а A = C ² / 4π, где C — заданная длина окружности.

Что такое периметр и площадь круга?

Длина окружности равна длине ее границы.Это означает, что периметр круга равен его длине окружности. Площадь круга равна πr ², а периметр / окружность — 2πr, когда радиус равен ‘r’. π составляет примерно 3,14 или 22/7. Окружность или радиус окружности важны для определения площади этого круга.

Для окружности радиуса «r» и окружности «C»:

π = Окружность / Диаметр
π = C / 2r
Следовательно, C = 2πr

Почему площадь круга равна πr

²?

Круг можно разделить на множество небольших секторов, которые затем можно соответствующим образом переставить в параллелограмм.Когда круг делится на еще более мелкие сектора, он постепенно приобретает форму прямоугольника. Мы ясно видим, что одна из сторон прямоугольника будет радиусом, а другая — половиной длины окружности, то есть π. Как мы знаем, площадь прямоугольника — это его длина, умноженная на ширину, которая равна π, умноженной на r. Следовательно, площадь круга равна πr ²

Какое значение имеет π?

Значение пи / π приблизительно равно 3.14. Пи — иррациональное число. Это означает, что его десятичная форма не заканчивается (например, 1/5 = 0,2) и не становится повторяющейся (например, 1/3 = 0,3333 …). Пи — 3,141592653589793238 … (всего с 18 знаками после запятой).

Как найти окружность и площадь круга?

Площадь и окружность круга можно рассчитать по следующим формулам. Окружность = 2πr; Площадь = πr ². Окружность круга может быть взята как π, умноженное на диаметр круга.А площадь круга в π раз больше квадрата радиуса круга.

Как рассчитать площадь круга с диаметром?

Диаметр круга в два раза больше радиуса круга. Следовательно, формула площади круга с использованием диаметра равна π / 4, умноженному на квадрат диаметра круга. Формула для вычисления площади круга с использованием диаметра круга π / 4 × диаметр ².

Как найти площадь круга по окружности?

Площадь круга также можно найти, используя длину окружности круга.Радиус круга можно найти по длине окружности круга, и это значение можно использовать для определения площади круга. Предположим, что окружность круга равна «C». Имеем C = 2πr или r = C / 2π. Теперь применив это значение «C» в формуле площади, мы получим A = πr ² = π × (C / 2π) ² = C ² / 4π.

Какова площадь круга радиусом 3 м?

Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга (A) при заданном радиусе r равна πr ².π составляет примерно 3,14 или 22/7. Следовательно, площадь = 3,14 х 3 х 3 = 28,26 кв. М.

Окружность данного круга составляет 16 см. Какая будет его площадь?

Окружность круга = 16 см

Мы знаем формулу длины окружности C = 2πr

Итак,

2πr = 16

или r = 16 / 2π = 8 / π

Подставляя значение r в формулу площади, получаем:

А = πr ²

A = π (8 / π) ² = 64 / π

На решении,

Площадь = 20. 38 кв. См.

Площадь круга — пояснения и примеры

Напомним, что область — это область, занимающая фигуру в двухмерной плоскости. В этой статье вы узнаете площадь круга и формулы для расчета площади круга.

Какова площадь круга?

Площадь круга — это мера пространства или области, заключенной внутри круга. Проще говоря, площадь круга — это общее количество квадратных единиц внутри этого круга.

Например, , если вы рисуете квадраты размером 1 см на 1 см внутри круга. Тогда общее количество полных квадратов, расположенных внутри круга, представляет площадь круга. Мы можем измерить площадь круга в м ², км ², в ², мм ^2, и т. Д.

Формула площади круга

Площадь круга можно рассчитать по трем формулам . Эти формулы применяются в зависимости от предоставленной вам информации.

Давайте обсудим эти формулы для определения площади круга.

Площадь круга с использованием радиуса

Учитывая радиус круга, формула для вычисления площади круга утверждает, что:

Площадь круга = πr ² квадратных единиц

A = πr ² квадратных единиц

Где A = площадь круга.

пи (π) = 22/7 или 3,14 и r = радиус круга.

Давайте лучше поймем эту формулу, решив несколько примеров задач.

Пример 1

Найдите площадь круга радиусом 15 мм.

Решение

A = πr ² квадратных единиц

Путем замены,

A = 3,14 x 15 ²

= (3,14 x 15 x 15) мм ²

= 706,5 мм ²

Итак, площадь круга 706.5 мм ²

Пример 2

Рассчитайте площадь круга, показанного ниже.

Решение

A = πr ² квадратных единиц

= (3,14 x 28 ²) см ²

= (3,14 x 28 x 28) см ²

= 2461,76 см ²

Пример 3

Площадь круга 254,34 квадратных ярда. Каков радиус круга?

Решение

A = πr ² квадратных единиц

254.34 = 3,14 x r ²

Разделите обе стороны на 3,14.

r ² = 254,34 / 3,14 = 81

Найдите квадратный корень из обеих частей.

√r ² = √81

г = -9, 9

Так как радиус не может иметь отрицательного значения, мы принимаем положительное 9 за правильный ответ.

Итак, радиус круга равен 9 ярдам.

Пример 4

Дождеватель лужайки разбрызгивает воду на 10 футов во всех направлениях при вращении.Какова площадь засыпанного газона?

Решение

Здесь радиус 10 футов.

A = πr ² квадратных единиц

= 3,14 х 10 ²

= (3,14 x 10 x 10) кв. Футов

= 314 кв. Футов

Таким образом, площадь засыпанного газона составляет 314 кв. Футов.

Площадь круга диаметром

Если диаметр круга известен, площадь круга равна,

Площадь круга = πd ²/4 квадратных единицы

Где d = диаметр круга.

Пример 5

Найдите площадь круга диаметром 6 дюймов.

Решение

A = πd ²/4 квадратных единицы

= 3,14 х 6 ²/4 кв. дюймы.

= (3,14 х 6 х 6) / 4 кв. в дюймах

= 28,26 кв. Дюймов

Итак, площадь круга диаметром 6 дюймов составляет 28,26 квадратных дюймов.

Пример 6

Рассчитайте площадь круга, показанного ниже.

Решение

Учитывая диаметр,

A = πd ²/4 квадратных единицы

= 3,14 х 50 ²/4

= (3,14 х 50 х 50) / 4

= 1962,5 см ²

Пример 7

Вычислите площадь обеденной тарелки диаметром 10 см.

Решение

A = πd ²/4 квадратных единицы

= 3,14 х 10 ²/4

= (3.14 х 10 х 10) / 4

= 78,5 см ²

Пример 8

Диаметр круглой тарелки 20 см. Найдите размеры квадратной тарелки, которая будет иметь ту же площадь, что и круглая тарелка.

Решение

Приравнять площадь круга к площади квадрата

πd ²/4 = с ²

3,14 x 20 ²/4 = s ²

с ² = 314

Найдите квадратный корень из обеих частей, чтобы получить,

с = 17.72

Следовательно, размеры квадратной тарелки будут 17,72 см на 17,72 см.

Пример 9

Найдите диаметр круга площадью 156 м ².

Решение

А = πd ²/4

156 = 3,14d ²/4

Умножьте обе стороны на 4.

624 = 3,14d ²

Разделите обе стороны на 3,14.

198,726 = d ²

д = 14.1 м

Таким образом, диаметр круга будет 14,1 м.

Площадь круга по окружности

Как мы уже знаем, длина окружности — это расстояние по окружности. Можно вычислить площадь круга по его длине.

Площадь круга = C ² / 4π

А = С ² / 4π

Где C = длина окружности.

Пример 10

Найдите площадь круга, длина окружности которого равна 25.12 см.

Решение

Учитывая окружность,

Площадь = C ² / 4π

А = 25,12 ² / 4π

= 50,24 см ²

Пример 11

Какова длина окружности окружности 78,5 мм ²?

Решение

А = С ² / 4π

78,5 = С ² / 4π

Умножаем обе стороны на 4π.

С ² = 985.96

Найдите квадратный корень из обеих частей.

C = 31,4 мм.

Итак, длина окружности 31,4 мм.

Предыдущий урок | Главная страница | Следующий урок

как вычислить площадь круга

Поскольку формула площади круга возводит в квадрат радиус , площадь большего круга всегда в 4 (или 2 ²) раз больше меньшего круга. Подумайте об этом: вы удваиваете число (что означает × 2), а затем возводите его в квадрат (то есть возводите в квадрат 2) — что приводит к новой области, которая в четыре раза меньше.

Вы можете убедиться, что это соотношение верно, если вы выберете некоторые фактические значения для радиуса круга.

Например, сделаем исходный радиус = 3.2 $$ A = $$ 9 \ pi $$ A = $$ 36 \ pi $$

$$ A_ {больше} = \ color {красный} {4} \ cdot A_ {меньше} \\ A_ {больше} = \ color {красный} {4} \ cdot 9 \ pi \\ A_ {больше} = 36 \ пи $$

Это соотношение сохраняется независимо от выбранного вами радиуса. 2 $$ A = $$ 25 \ pi $$ A = $$ 100 \ pi $$

$$ A_ {больше} = \ color {красный} {4} \ cdot A_ {меньше} \\ A_ {больше} = \ color {красный} {4} \ cdot 25 \ pi \\ A_ {больше} = 100 \ пи $$

Площадь круга | Формула для радиуса, диаметра и окружности

Содержание

Какова площадь круга?
Как найти площадь круга

Как рассчитать площадь круга

Площадь круга по окружности

Какова площадь круга?

Круг — это не квадрат, а площадь круга (количество внутреннего пространства, заключенного в круг) измеряется в квадратных единицах. Найти площадь квадрата несложно: длина умножена на ширину.

У круга, однако, есть только диаметр , или расстояние в поперечнике. У него нет четко видимой длины и ширины, поскольку круг (по определению) — это набор всех точек, равноудаленных от данной точки в центре.

Тем не менее, имея только диаметр или половину диаметра (радиус ), или даже только длину окружности (расстояние вокруг), вы можете вычислить площадь любого круга.

Как найти площадь круга

Напомним, что отношение длины окружности к ее диаметру всегда одно и то же, 3.14159265, пи или π. Это число, π, умноженное на квадрат радиуса круга, дает вам площадь внутренней части круга в квадратных единицах.

Формула площади круга

Если вам известен радиус r в любых единицах измерения (мм, см, м, дюймы, футы и т. Д.), Используйте формулу π r ² , чтобы найти площадь, A:

Ответом будут квадратные единицы линейных единиц, такие как мм2, см2, м2, квадратные дюймы, квадратные футы и так далее.

Вот круг радиусом 7 метров. Какая у него площадь?

[вставить чертеж круга шириной 14 м с обозначенным радиусом 7 м]

А = π · r2

А = π × 72

А = π × 49

A = 153,9380 м2

Площадь круга с использованием диаметра

Если вам известен диаметр d в любых единицах измерения, возьмите половину диаметра, чтобы получить радиус r в тех же единицах.

Вот проект недвижимости Сан-Сити, штат Аризона, круглого города диаметром 1.07 километров. Какой район Сан-Сити?

Сначала найдите половину заданного диаметра, чтобы получить радиус:

1,072 = 0,535 км = 535 м

Подставьте радиус в нашу формулу:

А = π · r2

А = π × 5352

А = π × 286,225

A = 899 202,3572 м2

Чтобы преобразовать квадратные метры, м2, в квадратные километры, км2, разделите на 1000000:

A = 0,8992 км2

Самый западный круглый жилой комплекс Сан-Сити имеет площадь почти 1 квадратный километр!

Как рассчитать площадь круга

Попробуйте эти вычисления площади для четырех разных кругов. Будь осторожен; некоторые указывают радиус r, а некоторые — диаметр d.

Не забудьте взять половину диаметра, чтобы найти радиус, прежде чем возводить радиус в квадрат и умножать на π.

Проблемы

Велосипедное колесо диаметром 406 мм
Колесо обозрения «Лондонский глаз», радиус 60 метров
Велосипедное колесо диаметром 26 дюймов
Самая большая пицца в мире имела радиус 61 фут 4 дюйма (736 дюймов)

Не ищите ответов, пока не произведете расчеты!

ответов

Велосипедное колесо диаметром 406 мм имеет радиус r 203 мм:

А = πr2

A = π × 203 мм2

А = 637.7433 мм2

Радиус 60 метров колеса обозрения «Лондонский глаз»:

А = πr2

A = π × 60 м2

A = 188,4955 м2

Велосипедное колесо диаметром 26 дюймов имеет радиус r 13 дюймов:

А = πr2

A = π × 13 дюйм2

A = 530,9291 дюйм2

Самая большая пицца в мире с радиусом 736 дюймов:

А = πr2

A = π × 736 дюйм2

A = 1 701 788,17 дюйм2

То есть 11817. 97 квадратных футов пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?

Площадь круга по окружности

Если вы не знаете, что такое радиус или диаметр, но знаете длину окружности C, вы можете все еще найти площадь.

Формула площади и окружности

Окружность (расстояние по окружности) находится по следующей формуле:

С = 2πr

Это означает, что мы можем взять формулу окружности и «решить для r», что даст нам:

г = C2π

Мы можем заменить r в нашей исходной формуле этим новым выражением:

А = π C2π2

Это выражение упрощается до следующего:

Эта формула работает каждый раз!

Как найти область по окружности

Вот красивая пиццы разумного размера, которую вы можете разделить с тремя друзьями.Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.

[вставить мультяшный рисунок типичной 16-дюймовой пиццы, но не указывать диаметр]

Замените C в формуле на 50,2655 дюйма:

А = 50.265524π

А = 2,526,62044π

A = 201,0620 дюйм2

Поровну разделите эту общую площадь для полноразмерной пиццы между четырьмя друзьями, и каждый из вас получит 50.2655 дюйм2 пиццы! Это примерно треть квадратного фута на каждого из вас! Ням ням!

Следующий урок:

Площадь сектора круга

Калькулятор площади круга

Калькулятор площади круга помогает вычислить поверхность круга с учетом диаметра или радиуса . Наш инструмент работает в обоих направлениях — неважно, ищете ли вы для вычисления площади или радиуса для области , вы нашли нужное место ◔

Мы познакомим вас с наиболее важной информацией, касающейся площади круга, его диаметра и радиуса. Мы узнаем , как найти площадь круга , поговорим о , формуле площади круга , и обсудим другие разделы математики, в которых используется то же уравнение.

Как рассчитать площадь круга? Формула площади круга

Итак, давайте посмотрим, как найти площадь круга. Есть несколько способов добиться этого. Здесь мы можем вычислить площадь круга , используя диаметр , или , используя радиус .

💡 Диаметр — это линия, которая пересекает центр фигуры и касается обоих ее краев.Радиус начинается в центре фигуры и заканчивается на краю фигуры.

Диаметр круга можно найти, умножив радиус круга на два:

Диаметр = 2 * Радиус

Площадь окружности радиуса. В калькуляторе радиуса круга используется следующая формула площади круга:

Площадь круга = π * r ²

Площадь диаметра круга. Калькулятор диаметра круга использует следующее уравнение:

Площадь круга = π * (d / 2) ²

Где:

π примерно равно 3,14 . Неважно, хотите ли вы найти площадь круга, используя диаметр или радиус — вам нужно будет использовать эту константу почти в каждом случае.

Теперь, когда вы знаете, как рассчитать площадь круга, мы рекомендуем вам попробовать другие наши калькуляторы кругов:

> Сектор круга — это сечение круга между двумя радиусами.Вы можете думать об этом как о гигантском куске пиццы. > Это «отрезанная» часть круга, ограниченная хордой или секущей. > Это угол с вершиной в центре, руки которого доходят до окружности.

Как использовать калькулятор площади круга? Диаметр к площади и радиус к площади.

Вы можете легко вычислить все, площадь круга, его диаметр и радиус, , используя наш калькулятор площади круга в мгновение ока:

Определите , является ли ваше заданное значение диаметром или радиусом , используя изображение справа и определения, доступные в разделе выше (вы можете рассчитать площадь круга, используя диаметр, а также радиус) .
Введите значение в соответствующее поле калькулятора .
Это не заняло много времени — ваши результаты здесь ! Мы решили включить пошаговое решение и все самые важные данные прямо под калькулятор.

Вот как быстро вычислить площадь круга 😉

Зачем нам нужны калькуляторы площади круга?

Площадь круга, определенная калькуляторами радиуса и диаметра , служит основой для многих других уравнений — не только в математике, но и в повседневной жизни! Вот несколько примеров, когда знание того, как найти площадь круга, может быть полезно:

Нам нужно знать площадь поверхности круга, чтобы рассчитать объем конуса и его площадь 🎉
Ваша вечеринка с пиццей была бы неполной без нашего инструмента для пиццы на основе калькулятора диаметра и площади
Мы используем вычисления, подобные этому, при получении информации о сфере, например, об объеме сферы. 000
Вам нравятся красивые платья? Может вы любите шить ? Откройте для себя наш калькулятор для круглой юбки! Эффективное шитье еще никогда не было таким простым. 000

Кругов: Площадь

А круг — это множество всех точек на плоскости на заданном расстоянии (называемое радиус ) из заданной точки (называемой центром).

Отрезок, соединяющий две точки на окружности и проходящий через центр, называется отрезком. диаметр круга.

Очевидно, что если d представляет длину диаметра и р представляет длину радиуса, тогда d знак равно 2 р .

В длина окружности C круга — это расстояние по внешней стороне. Для любого круга эта длина связана с радиусом р по уравнению

C знак равно 2 π р

где π (произносится » Пи «) является иррациональный константа примерно равна 3. 14 .

В область круга задается формулой

А знак равно π р 2 .

Пример 1:

Какова площадь круглого стола диаметром 6 футов?

При этом диаметр круглого стола равен 6 футов

Итак, радиус круглого стола равен половине диаметра.То есть радиус 3 футов

Используйте формулу для площади круга, А знак равно π р 2 , где р это радиус круга.

Заменять 3 для р в формуле.

А знак равно π ( 3 ) 2 знак равно π ( 9 ) ≈ 28. 26

Следовательно, площадь круглого стола составляет около 28,26 футов 2

Пример 2:

Какова площадь заштрихованной области на показанном рисунке?

Ясно отмечено, что больший круг имеет радиус 11 см. Итак, его площадь составляет

А большой круг знак равно π р 2 знак равно π ( 11 ) 2 знак равно 121 π ≈ 379. 94 см 2

А как насчет меньшего круга? Ну а расстояние от центра до края 11 см; диаметр меньшего круга 11 — 4 знак равно 7 см. Итак радиус меньшего круга 3.5 см.

А маленький круг знак равно π р 2 знак равно π ( 3.5 ) 2 знак равно 12,25 π ≈ 39.