Уклон 12%, сколько это в градусах?
12% от 90 градусов.
360 — 100%, дальше сам
примерно 7 град
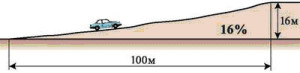
Уклон дороги — относительное превышение одной точки продольного (поперечного) профиля дороги над другой, определяемое как отношение превышения к горизонтальному расстоянию между двумя точками. Уклон 10% Это отношение высоты подъёма в 10 метров к горизонтальной проекции дороги длинной 100метров. В геометрическом смысле — это тангенс угла подъёма дороги. Чтобы перевести уклон из процентов в градусы надо уклон дороги в процентах разделить на100 и полученную велину посмотреть в таблице Брадиса раздел Тангенсы. <a href=»/» rel=»nofollow» title=»11898030:##:http://www.webmath.ru/poleznoe/table_tg.php» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> Для уклона 10% угол уклона в процентах будет примерно tg(6°) -0.105 Шесть градусов. Для уклона 100% угол наклона 45 градусов.
Это надо понимать также, как говорят: скидка цен на товары 40%, спрашивается от двух милионов скидывают или от трёх, а другой спрашивает, с какого этажа скидывают с пятого или с девятого?
Уклон в процентах часто используют для обозначения уклона дорог или строительных объектов. Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т. е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона.
12% — 5.4 градуса. Процент считается от 45%.
Мозги людям пудрите, арктангенс (12%/100%)=6,84
touch.otvet.mail.ru
Уклон в градусах и процентах
Горнолыжные градиенты или о крутизне синих, красных и черных трасс
Поговорим об уклонах
На практике крутизна наклонной поверхности в различных областях человеческой деятельности обозначается величиной уклона (или еще иначе — градиентом). Для начала давайте разберемся, что же означает само это понятие. Таблички с указанием уклона знакомы, наверное, всем водителям автомобилей (по крайней тем, кто самостоятельно сдал хотя бы теорию), но далеко не все из них знают, что же фактически означает, например, 10% на знаке.
Кто-то по-простому думает, что это угол наклона дороги, то есть 10 градусов. Некоторые идут дальше в своих размышлениях и считают, что это доля от максимально возможного угла подъема в 90 градусов (отвесная стена) и 10% — это 90°×0.1 = 9°. Мы все привыкли мыслить в градусах, каждый может визуально представить себе 90 градусов, 45, 30 и т.д., поэтому и стремимся все воспринимать в этой единице измерения (а правильный ответ: 10% = 5.7°).
На самом деле математически уклон — это отношение перепада высоты на определенном участке пути к длине горизонтальной проекции этого пути, выраженное в процентах. Т.е. высота (h), разделенная на проекцию пути (c) и умноженная на 100. Геометрически это отношение противолежащего катета к прилежащему (тангенс, умноженный на 100). Таким образом:
Уклон в процентах (градиент) = h/c×100 = tg(a)×100
Ниже представлена форма, позволяющая перевести значения из градиентов в градусы и обратно:
Градиенты % = Градусы °
Ближе к делам горнолыжным
С теорией разобрались, переходим к горнолыжной практике.
Профиль горнолыжной трассы никогда не представляет из себя идеальную прямую. Где-то наклон может быть покруче, где-то поположе.
Уклон кровли в градусах и процентах
В этом случае используется понятие среднего градиента, который, впрочем, вычисляется все по той же формуле: перепад высот между стартом и финишем трассы, деленный на длину горизонтальной проекции трассы.
По статистике средние градиенты синих трасс находятся в пределах до 18% (порядка 10 градусов), красных — до 23% (13 градусов), а черных — от 23% и выше (больше 13 градусов). На каких-то курортах сложность трасс несколько занижена (синие трассы в реальности могут оказаться ближе к красным по крутизне), на каких-то наоборот, ее завышают, но в среднем картина везде примерно такая.
Для ориентировочной оценки длин трасс, катаясь на курорте и имея на руках схему катания с обозначением перепадов высот, вы можете использовать следующие соотношения:
На каждый километр перепада высоты синей трассы приходится порядка 7 км ее длины, на километр перепада красной — 5 км, черной — 3.5 км.
Ниже на картинке для сравнения представлены профили синей, красной и черной трасс. Трассы находятся в известнейшем итальянском регионе Селларонда, а профили их взяты из замечательного приложения 3D Dolomiti Superski, которое позволяет совершить виртуальный тур по региону, а также посмотреть технические характеристики всех трасс.
| Название трассы | Длина | Перепад | Наклон | Градиент |
|---|---|---|---|---|
| Piz Seteur | 2050 м | 204 м | 5.7° | 10.0% |
| Fermeda 1 | 2090 м | 456 м | 12.6° | 22.4% |
| Gran Risa | 2290 м | 677 м | 17.2° | 30.9% |
Отдельно отметим представленную на картинке Gran Risa — знаменитую трассу, входящую в пятерку культовых трасс Кубка мира. Глядя на ее профиль можно подумать, что ничего такого особенного в нем нет, но на деле, когда вы оказываетесь на трассе, в некоторых местах может показаться, что склон уходит вертикально вниз.
Этот эффект часто присутствует при сравнении профиля трассы с реальной обстановкой на местности. Также не будем забывать, что мы все время ведем речь о средних градиентах, в то время как некоторые локальные участки склона могут оказаться намного круче (и часто именно по этим самым крутым местам присваивают сложность трассе).
Харакири
В австрийском Майрхофене находится одна из самых крутых трасс мира (и самая крутая в Австрии), с говорящим названием Harakiri. Ее средний уклон составляет 78% (38°, длина около 620 метров при перепаде 380 метров). Для подготовки склона используется специальная техника, закрепленная на спущенных сверху страховочных канатах.
Падение на Harakiri может быть чревато тем, что до конца трассы вы будете катиться кубарем, не имея возможности затормозить.
Так что всегда, катаясь на лыжах, соизмеряйте свои возможности с предлагаемыми горами условиями. Берегите себя и окружающих лыжников!
  При решении геодезических и инженерных задач, очень часто приходиться вспоминать и искать необходимые формулы. В связи с этим хочется представить Вам шпаргалку (назовем её “геодезической шпаргалкой”:)), в которой приведены часто использующиеся формулы.
  Конечно, ее содержание не охватывает всю высшую математику или сферическую геометрию, но что-нибудь должно пригодиться.
  Зная из собственного опыта, неудобство восприятия формул без чисел, к каждой из них приводится пример вычисления.
Пример вычислений теорема Пифагора
Пример вычислений соотношения в прямоугольном треугольнике
— арксинус (arcsin) возвращает угол по его синусу
— арккосинус (arccos) возвращает угол по его косинусу
— арктангенс (arctg) возвращает угол по его тангенсу
— арккотангенс (arcctg) возвращает угол по его арктангенсу
Пример вычислений обратные тригонометрические функции
Сумма углов в треугольнике равна 180 градусам
Для любого треугольника соблюдается выражение
Пример вычислений теорема синусов
  Квадрат любой стороны треугольника, равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними
Пример вычислений теорема косинусов
  Площадь треугольника можно определить по формулам
также удобно использовать формулу Герона 
, где p-полупериметр треугольника 
Пример вычислений площадь треугольника
или по формуле Герона
  Длина дуги окружности вычисляется по формулам
если угол задан в угловых градусах минутах и секундах
если угол задан в радианах
Пример вычислений длина дуги окружности
угол задан в угловых градусах минутах и секундах
угол задан в радианах
  Перевод угловых градусов минут и секунд в градусы выполняется согласно выражения
Пример вычислений
перевести в градусы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод минут и секунд угла в градусы онлайн   Перевод градусов в угловые градусы минуты и секунды выполняется согласно выражения
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в градусах
Смотрите перевод градусов угла в минуты и секунды онлайн   Перевод градусов в радианы выполняется по формуле
Пример вычислений
перевести в радианы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод градусов в радианы онлайн   Перевод радианов в градусы выполняется по формуле
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в радианах
Смотрите перевод радиан в градусы онлайн   Определение наклона линии в градусах выполняется с использованием соотношений в прямоугольном треугольнике Пример вычислений
  Определить наклон пандуса длиной 14м и высотой 3,5м
  При инженерно-строительных работах, наклон линии задают не градусом наклона, а тангенсом этого градуса — безразмерной величиной, которая называется уклоном. Уклон может выражаться относительным числом, в процентах (сотые доли числа) и промилле (тысячные доли числа)
Пример вычислений
  Определить уклон отмостки длиной 2,5м и высотой 0,30м
astgift.ru
Уклоны. Теория — на уровне глаз — ЖЖ
Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).
Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой). Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.
Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.
Причины: почему проценты?
При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:
а) КартыТак проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.
Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.
б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.
в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).
seyfulmulyukov.livejournal.com / 1avtorul.ru
Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]
Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.
Использованные материалы
1. Словари и энциклопедии на Академике © Академик2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3. Википедия © Wikipedia
—
gre-kow.livejournal.com
| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | 8^2 | |
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
www.mathway.com
Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
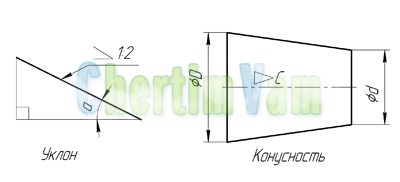
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
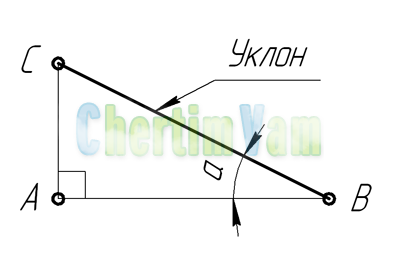
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
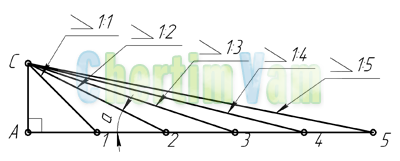
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
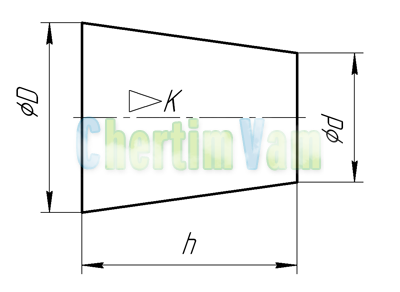
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
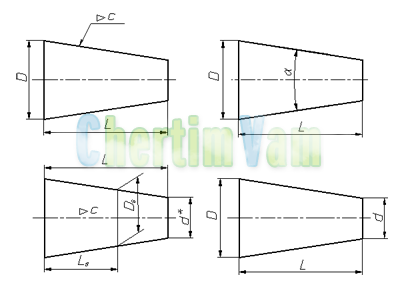
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
chertimvam.ru